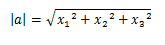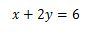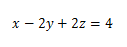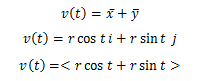BAB VI KOORDINAT KARTESIUS, VEKTOR DAN PERSAMAAN BIDANG DALAM RUANG DIMENSI

A. KOORDINAT KARTESIUS DALAM RUANG DIMENSI

Patokan mula yang diambil dalam koordinat kartesius dimensi tiga adalah tiga garis lurus saling tegak lurus yang di namakan sumbu x, sumbu y, dan sumbu z. Ketiga sumbu tersebut menentukan tiga bidang, yaitu bidang xy, bidang xz, dan bidang yz. Ketiga bidang ini membagi ruang menjadi delapan oktan, yaitu oktan-oktan I, II, II,...VIII.

Gambar 1. Koordinat Kartesius Ruang Dimensi Tiga

Ket:

Sumbu x = absis

Sumbu y = ordinat

Sumbu z = aplikat

Oktan-oktan I, II, III, dan IV berada diatas bidang xy

Oktan-oktan V, VI, VII, dan VIII berada dibawah bidang xy

POSISI TITIK PADA KOORDINAT KARTESIUS RUANG DIMENSI

Gambar 2. Posisi Titik Pada Koordinat Kartesius Ruang Dimensi Tiga

Titik O(0,0) disebut titik asal. Setiap pada sumbu x, ordinat dan aplikatnya nol, sedang suatu yang terletak pada bidang xy, aplikatnya nol.

Untuk menggambar sebuah titik, kita tidak perlu menggambar balok, tetapi cukup dengan tiga ruas garis yang menyatakan panjang absis, ordinat dan aplikatnya.

JARAK ANTAR TITIK PADA RUANG DIMENSI TIGA

Gambar 3. Jarak Antar Titik

Rumus jarak antara A(x₁, y_1, z₁) dan C(x₂, y_2, z₂)

B. VEKTOR PADA RUANG DIMENSI

Gambar 4. Vektor pada koordinat kartesius dimensi tiga

Dalam ruang-ruang dimensi tiga suatu titik dinyatakan dengan tiga komponen, yaitu absis, ordinat dan aplikat. Misalnya B(x₁, y_1, z₁). Vektor posisi (terhadap titik O) untuk titik B adalah a = < x₁, y_1, z₁> = x₁i, y₁j_, z₁k.

Vektor-vektor basis i,j,k berturut-turut adalah vektor-vektor satuan yang searah dengan sumbu-sumbu x positif, y positif dan z positif.

Semua sifat penjumlahan vekotr dan perkalian vekotr dengan skalar yang berlaku dalam bidang datar juga berlaku untuk vektor dalam ruang dimensi tiga.

PANJANG VEKTOR

Jika a = < x₁, y_1, z₁> maka panjang vektor a adalah,

PERKALIAN TITIK PADA VEKTOR

Jika u = < u₁, u_2, u₃> dan v = < v₁, v_2, v₃>, maka perkalian titiknya didefinisikan sebagai berikut

Dengan θ adalah sudut yang dibentuk oleh u dan v dan serta 0 ≤ θ ≤ phi

Dari definisi diatass didaptkan rumus sudut yang dibentuk oleh vektor u dan v yaitu,

PERKALIAN VEKTOR

Jika u = < u₁, u_2, u₃> dan v = < v₁, v_2, v₃> maka perkalian kedua vektor adalah,

HASIL KALI SILANG DUA VEKTOR

Perkalian silang dua vektor a = a₁i + a₂j + a₃k dan b = b₁i + b₂j + b₃k didefinisikan sebagai berikut,

Dengan θ adalah sudut yang dibentuk kedua vektor dan u adalah vektor satun yang tegak lurus pada a dan b.

C. PERSAMAAN BIDANG DATAR

Persamaan linier bidang datar ialah,

Dengan A, B, C ≠ 0

Persamaan umum bidang yag melalui P(x₁, y_1, z₁) dan tegak lurus pada vektor n = <A,B,C> adalah

Jika diketahui dua bidang, yaitu A₁x + B₁y + C₁z = D dan A₂x + B₂y + C₂z = D, maka:

1.Jika θ adalah suatu sudut antara dua bidang ini, maka

 2.      Dua bidang tersebut saling tegak lurus, apabila

3.      Dua bidang tersebut sejajar, apabila

 4.      Dua bidang tersebut berimpitan, apabila

Jika d adalah jarak titik P(x₁, y_1, z₁) ke bidang Ax + By + Cz = D maka

Contoh:

Persamaan bidang yang melalui P(1,2,3) dan tegak lurus n = <3,2,1> adalah

Maka, persamaan bidangnya,

TUGAS

Apakah terdapat titik potong pada persamaan berikut:

Bidang P(1,2,3) Tegak Lurus dengan vektor n = <3,2,1>

Penyelesaian:

untuk

Titik potong terhadap sumbu x, maka z = 0

x = 6

sehingga (6,0,0)

Titik potong terhadap sumbu z, maka x = 0

z = 3

sehingga (0,0,3)

untuk

Titik potong terhadap sumbu x, maka y = z = 0

x = 4

sehingga (4,0,0)

Titik potong terhadap sumbu y, maka x = z = 0

y = -2

sehingga (0,-2,0)

Titik potong terhadap sumbu z, maka x = y = 0

z = 2

sehingga (0,0,2)

Dari persamaan bidang (1,2,3) tegak lurus vektor n = <3,2,1> didapatlah persamaannya:

Titik potong terhadap sumbu x, maka y = z = 0

x = 3,3

sehingga (3,3;0;0)

Titik potong terhadap sumbu y, maka x = z = 0

y = 5

sehingga (0,5,0)

Titik potong terhadap sumbu z, maka x = y = 0

z = 10

sehingga (0,0,10)

Dari penyelesaian di atas, terbentuklah tiga bidang, dan tiga bidang tersebut bertemu di suatu titik, maka dapat disimpulkan bahwa tiga bidang yang terbentuk memiliki titik potong.

Read More

BAB V VEKTOR PADA BIDANG DAN PERSAMAAN PARAMETRIK

A. VEKTOR PADA BIDANG

Gambar 1. Vektor

Vektor adalah himpunan ruas garis berarah yang mempunyai besar dan arah yang sama.

dalam literaturad beberapa simbol untuk wakil vektor antara lain

1.      Dengan satu huruf kecil a,b,c,... yang dicetak tebal, atau

2.  Dengan dua huruf besar dengan tanda anak panah di atasnya. Anak panah tersebut menyatakan arah, misalnya. vektor AB, Vektor ini dimaksudkan vektor dengan titik pangkal A dan titik ujung B. Vektor ini dinamakan vektor bebas.

Suatu vektor yang titik pangkal tertentu dan vektor-vektor vekor lainnya harus mempunyai titik pangkal tertentu dinamakan vektor posisi.

Gambar 2. Vektor Posisi

VEKTOR PADA KOORDINAT KARTESIUS

Gambar 3. Vektor Pada Koordinat Kartesius

PENJUMLAHAN VEKTOR

1.      Cara Jajaran Genjang 

Penjumlahan dua buah vektor dilakukan dengan mengimpitkan kedua pangkal vektor tersebut, kemudian buat garis yang panjangnya masing-masing sama dengan panjang vektor semula sehingga membentuk jajaran genjang. Maka hasil dari penjumlahan kedua vektor tersebut adalah vektor yang pangkalnya pada titik pangkal kedua vektor tersebut dan ujungnya adalah pada perpotongan kedua garis tersebut.

Gambar 4. Penjumlahan Vektor cara Jajar Genjang

b. Cara Segitiga

Impitkan titik ujung vektor a dengan titik pangkal vektor b, maka vektor hasil penjumlahannya adalah vektor yang bertitik pangkal di a dan titik ujungnya di b.

Gambar 5. Penjumlahan Vektor cara Segitiga

PENGURANGAN VEKTOR

Lawan dari vektor a adalah vektor –a, yang mempunyai besar yang sama dengan a tapi berlawanan arah. Maka pengurangan vektor adalah dengan menjumlahkan dengan lawan vektor kedua, yaitu  a – b = a + (-b)

Contoh:

PERKALIAN VEKTOR

Contoh:

Sifat-sifat Penjumlahan dan Pengurangan Vektor:

1. a + b = b + a

2. a + (b + c) = (a + b) + c

3. a + b = c    jika dan hanya jika b = c – a

4. a + 0 = a, a – a = 0

5. k(sb) = (ks)b = b(ks)

6. k(a + b) = ka + kb

7. (k + s)a = ka + sa

8. 1a = a

PERSAMAAN VEKTOR UNTUK SUATU GARIS LURUS

Perhatikan gambar, diketahui titik D(d_1,d₂) dan sebuah vektor u = <u₁,u₂>

Gambar 6. Persamaan Vektor Suatu Garis

Kita akan menentukan persamaan vektor garis l yang melalui titik D dan sejajar dengan u. Vekor posisi titik D terhdap titik O adalah < d_1,d₂> = d.

Ambil sembarang titik W(x,y) pada garis l, maka vektor letak titik W terhadap O adalah w = <x,y>

Perhatikan bahwa,

Karena garis l sejajar u dan vektor DW pada l, maka vektor DW sejajar u sehingga ada bilangan real(skalar) k sedemikian hingga,

Persamaan diatas disebut persamaan vektor gais yang memalui titik D dan sejajar dengan u.

Contoh:

Tentukan persamaan vektor suatu garis yang melalui A(3,-5) dan B(1,2) dan tentukan persamaan kartesiusnya

Gambar 8. Contoh Soal

Persamaan kartesius

PERSAMAAN VEKTOR SUATU LINGKARAN

1. Lingkaran berpusat di O(0,0) dan berjari-jari r

Gambar 9. Persamaan Vektor Pada Lingkaran berpusat di (0,0)

persamaan vektor nya adalah,

2. Lingkaran berpusat di P(a,b) dan berjari-jari r

Gambar 10. Persamaan Vektor Pada Lingkaran berpusat di (a,b)

Persamaan Vektor nya adalah,

B. PERSAMAAN PARAMETRIK

Persamaan parametrik suatu kurva daoat dinaytakan ke dalam persamaan kartesius dengan cara menlenyapkan parameternya, untuk melenyapkan paramternya, kadang menggunakan cara subtitusi atau menggunakan hubungan parameternya.

Setiap persamaan kartesius apat dinyatkan sebagai persamaan parameter dan sebaliknya kadang-kadang suatu kurva dapat dinyatakan dengan persamaan parameter syang sederhana, tetapi jika dinyatakan dalam persamaan kartesis menjadi lebih rumit. Kurva dari suatu persamaan parametrik merupakan kurva berarah.

Bentuk umum persamaan parametrik dari suatu kurva bidang adalah

Dengan:

a , b € R dan t parameternya.

Read More