Hiperbola adalah himpunan titik-titik yang
selisih jaraknya terhadap dua titik tertentu tetap besarnya.
a. Hiperbola dengan
horizontal major axis
Gambar 1. Elips Horizontal Major Axis
KET:
F1 dan F2 adalah titik fokus
hiperbola
A dan B adalah titik-titik puncak
Dari
definisi hiperbola, kita dapat mencari persamaan hiperbola. Misalkan
titik-titik fokus, F1,F2 pada sumbu x dan sumbu dari F1F2
adalah sumbu y. Jika |F1F2| = 2c maka F1(-c,0)
dan F2(c,0). Misalkan selisih jarak yang tetap itu adalah 2a dengan
a < c.
Dengan
P(x,y) sebarang titik yang memenuhi definisi, yaitu:
b. Hiperbola dengan Vertical Major Axis
Gambar 2. Elips Vertical Major Axis
Persamaan
hiperbola dengan vertical major axis adalah,
GARIS SINGGUNG HIPERBOLA
Gambar 3. Garis Singgung Hiperbola
Selanjutnya, kita mencari persamaan garis singgung
pada hiperbola denfan jalan yang sama seperti persamaan garis singgung pada
elips.
Misalkan
persamaan garis yang gradiennya m
adalah y = mx + p maka persamaan garis singgungnya:
Garis
akan menyinggung elips jika titik-titik potongnya berimpit. Hal ini terjadi
apabila persamaan kuadrat di atas mempunyai dua kara yang sama atau apabila diskriminannya sama dengan nol.
Jadi,
persamaan garis singgung yang gradiennya m adalah,
PERSAMAAN GARIS SINGGUNG DI TITIK PUSAT
(α,β)
Misalkan
persamaan hiperbola
Dengan
menggunakan tarnslasi susunan sumbu, kita memperoleh persamaan garis singgung
pada elips yang berpusat P(α,β)
dengan gradien m adalah







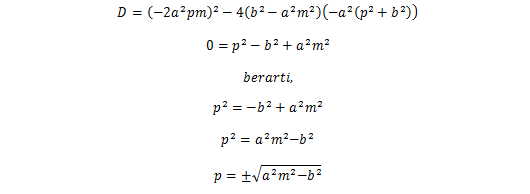



0 komentar:
Posting Komentar